最近,华为公司总裁任正非表示,这几年华为加大了海外留学生的招聘力度,现在要关注“高鼻子”人才的获取,给予海外研究所更多的预算。
而今年9月,就有一位数学家加入华为,他就是法国数学家、菲尔兹奖得主洛朗·拉福格。
1
洛朗·拉福格到底是谁
众所周知,诺贝尔奖中未设数学奖,但在数学界有一项与诺贝尔奖同等声誉的国际数学大奖,那就是菲尔兹奖。它在每四年举行一次的国际数学家大会上隆重颁发,获奖者都是年龄不超过40岁的数学精英。
而洛朗·拉福格由于他在朗兰兹纲领研究方面取得了巨大进展,证明了与函数域情形相应的整体朗兰兹纲领,于2002年荣获菲尔兹奖,时年35岁。
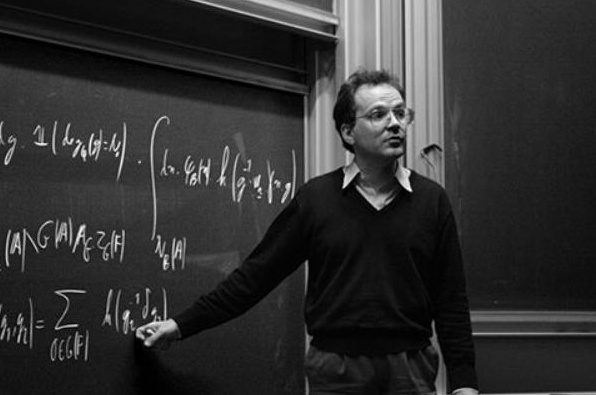
拉福格是法国数学家,1966年11月6日生于法国的安托尼。1986—1990年在巴黎高等师范学院学习,1994年获博士学位,2000年成为位于法国伊沃特布雷的高等科学研究院终身教授。
他的兴趣爱好很广泛,小时候曾经是个文学迷,梦想当一名作家。
但他的数学成绩也很好,在数学上表现出众,因此逐渐“发现”了自己也有数学天赋,终于把达到了痴迷程度的文学兴趣转移到数学上来了。
2
何为朗兰兹纲领?
拉福格获得菲尔兹奖是因为他在朗兰兹纲领研究上作出了巨大贡献,使得数论与分析学两大领域之间建立起了一个新的联系,同时还发现了一种可能会被证明十分重要的新的几何构造。目前这些成果的影响正波及整个数学领域。
那么到底什么是朗兰兹纲领呢?
朗兰兹纲领是加拿大数学家朗兰兹 1967年在给法国数学大家韦伊的一封著名的信函中提出的。它是一组意义深远的预测性猜想和知识性见解。它预言所有主要数学领域之间原本就存在着一种统一的联结。依赖它,数学家在一个领域不能解决的问题,可以转到另一个领域去解决,如果仍然难以找到答案,还可以转到又一个领域中去解决……直至问题被彻底解决为止。

虽然朗兰兹未给出相关证明,因此朗兰兹纲领仍只能算是猜想。但这不影响朗兰兹纲领的重要性和对数学的影响。
而拉福格在前人的系列工作的基础上作出的进一步突破——对整体的朗兰兹纲领给出了一个完整的理解,同时还发现了一个十分具有前景的新的几何结构。
拉福格的创造性在于,他证明了:“对于函数域上的一般线性群 Gr(r ≥ 1),存在唯一保持 L 逐数的一一对应。”他的工作对任意给定的函数域(比如所有多项式之商形成的“有理式集”是一种函数域),精确地建立起了它的伽罗瓦群表示与其相应的一个自守形式(或称模形式)之间的联系。
当然,朗兰兹纲领猜测的最后证明尚未完成,它仍然是 21 世纪最大的难题之一,也是今后很有潜力的研究领域之一,而目前拉福格仍然是这一领域的领先者。
3
与中国之缘
2002年拉福格曾经到北京参加第24届国际数学家大会,当时,他除了在大会上作一小时大会报告外,还于8月27日晚上应邀参加了北京师范大学举行的第24届国际数学家大会的部分代表晚宴,他还兴致勃勃地为北京师范大学数学系题词,他说:“北京之行给我留下了深刻印象,人们对数学、科学、学习的热情令人惊讶,我衷心希望中法两国的数学家进一步增进交流,并希望再次访问中国。”
也许,这也是他与华为结缘的一个铺垫?

如果你想了解更多关于拉福格和获得菲尔兹奖的数学家的信息,欢迎翻开《当代数学精英——菲尔兹奖得主及其建树与见解(第三版)》,本书对历年菲尔兹奖得主,按获奖先后逐一编写,其内容包括姓名,照片,国籍,出生年、月、日及地点,主要简历和学术职务,获奖成果,并对该获奖者获奖领域的有关知识及发展状况作了适当介绍,特别是引用了一些著名数学家对该获奖者的评论,同时介绍了该获奖者对数学、数学研究或数学教育的一些精辟见解等。

《当代数学精英
——菲尔兹奖得主及其建树与见解(第三版)》
李心灿 高隆昌 邹建成 郑权 张静 编
上海科技教育出版社
转自【上海科技教育出版社】
