今年春晚

魔术师刘谦表演了

一个与纸牌相关的魔术

精妙的设计带给观众极高的参与感

许多人纷纷拿出家中的扑克牌

跟着刘谦一起“见证奇迹”

主持人尼格买提

在春晚舞台上参与魔术

但没能将扑克牌对上

当晚，“小尼的扑克牌没对上”

就登上了微博热搜

撒贝宁称他是

“全国唯一一个（没对上）”

网友笑说

他的这一失误“承包了一年的笑点”

大年初三

“小尼的失误被警方当成典型案例了”

的词条再度登上热搜

小尼也再发微博

向央视文艺和春晚提问：

“大概还要重播几次？我就问问。”

央视文艺在这条微博下回应道：

“再播亿遍”。

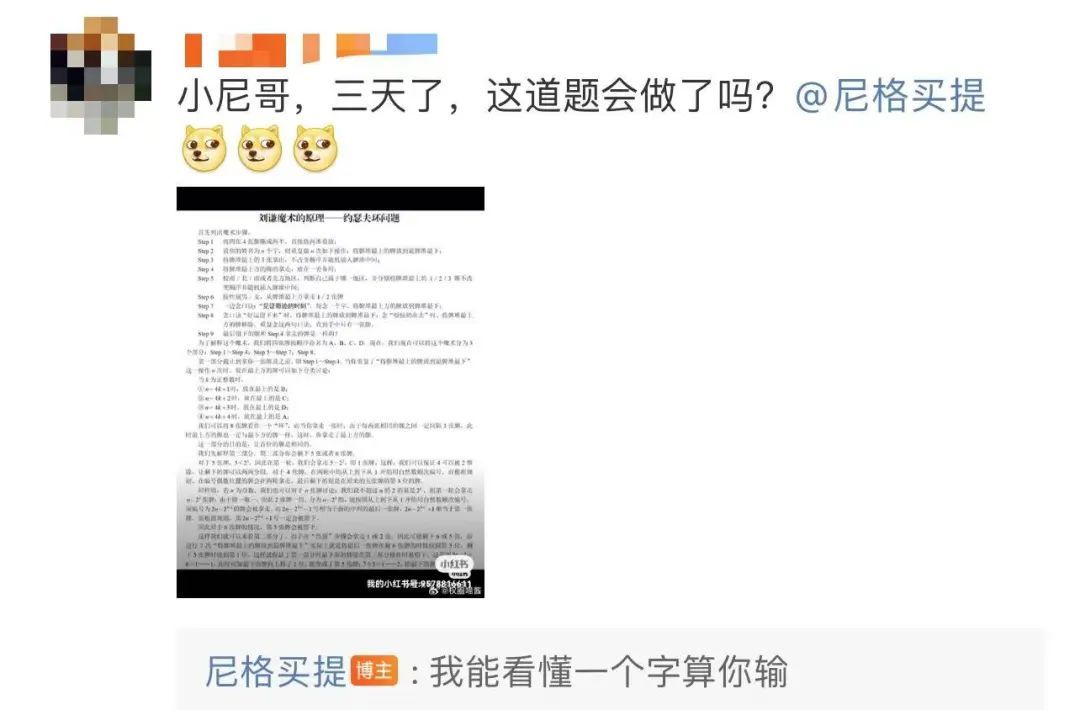
还有网友发出魔术的“解题步骤”

灵魂发问：

“小尼哥，三天了，

这道题会做了吗？”

小尼表示：

“我能看懂一个字算你输。”

那么问题来了

这个魔术“奇迹”的背后

有着怎样的奥秘？

其实是一个数学

“约瑟夫问题”

随后

北京大学、吉林大学

也相继发文

解释了“约瑟夫问题”

先来看看北京大学的“揭秘”：

什么是“约瑟夫问题”？

北大文中解释：

设有编号为1，2，......，n的n个人围成一个圈，从第1个人开始报数，报到m时停止报数，报m的人出圈。再从他的下一个人起重新报数，报到m时停止报数，报m的出圈......按照这个规则进行下来，直到所有人全部出圈为止。求最后留下来的人编号。

为了使问题简化，我们考虑n个人编号为0 ~ n-1的情况，每 m 个人退出一个人，我们称之为（n, m）问题。

第一个人（即编号为在模n下同余m的人）退出之后，对剩下的 n-1 个人重新编号，则新问题的k号在原问题中对应 k+m 号。因此（n, m）问题的解 j (n, m) = j (n-1, m)+m 且 j (1, m) = 0（模n意义下）。据此，通过递推的方法可以得到 j (n, m)。

“在实践中

约瑟夫问题一般用代码进行求解

刘谦的魔术中使用的

便是m=2 的特殊情况”

再来看看吉林大学的“揭秘”：

看了这一“揭密”

有网友笑称

“魔术的尽头是数学”

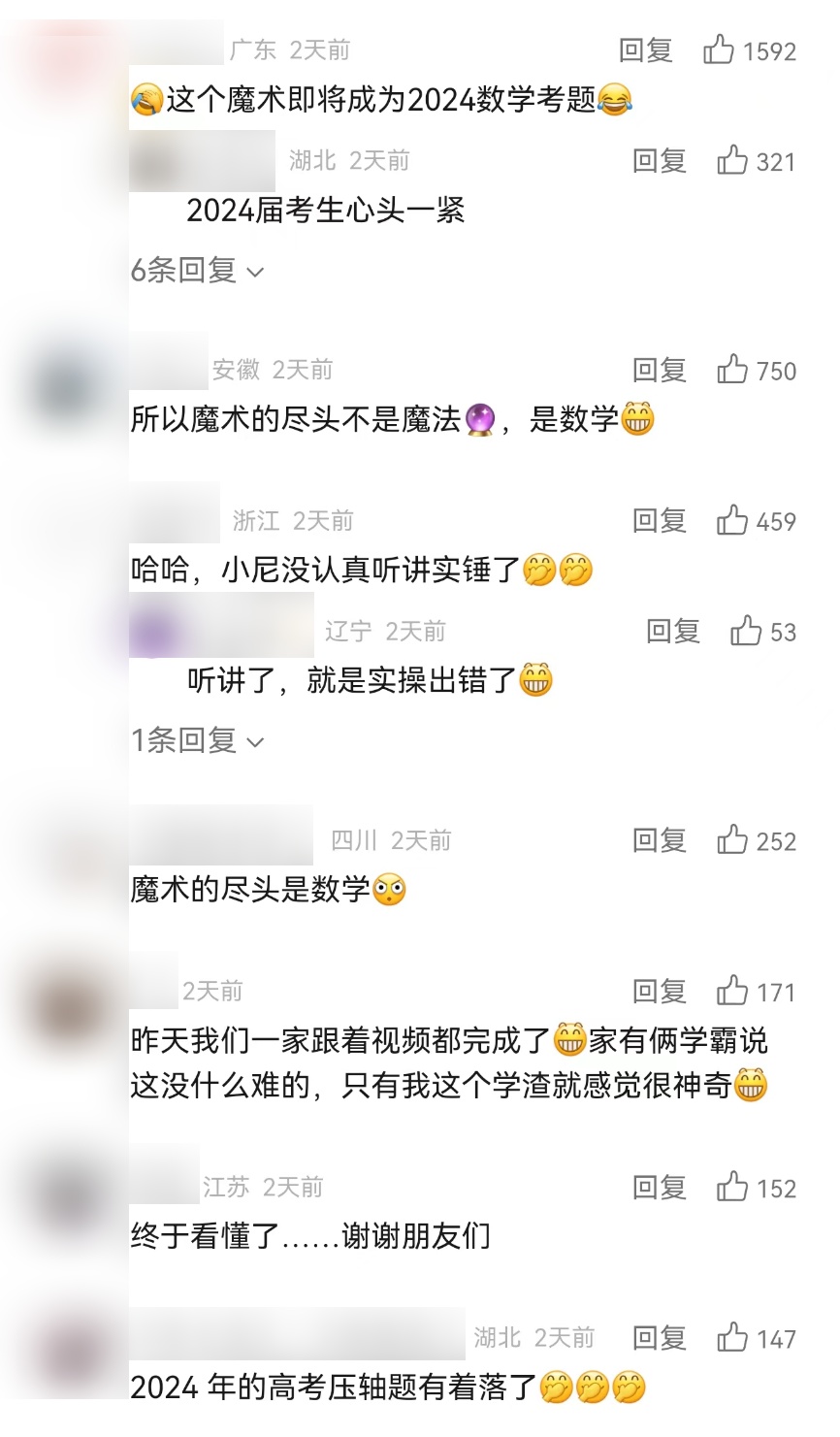
这个魔术，你看懂了吗？

图文来源：升学宝，综合自@平安北京、@尼格买提、中国青年报、@央视文艺、极目新闻、红星新闻、澎湃新闻、网友评论等

关注：请点文章主标题下“东方教育时报”

或查找搜索公众账号

=== 从教育的视角看社会 | 从社会的视角看教育 ===

上观号作者：东方教育时报